| √ | |||
kalkulator pierwiastków - Pierwiastek sześcienny, Pierwiastkowanie
kalkulator pierwiastków
Treści
Z naszym kalkulator pierwiastków możesz obliczyć rodniki niezależnie od wartości ich indeksu czy radicandu. Oprócz obliczania pierwiastków ten kalkulator jest również świetnym upraszczającym radykalne krok po kroku, dzięki czemu możesz łatwo nauczyć się procesu upraszczania rodników.
Instrukcja korzystania z kalkulator pierwiastków
Aby uprościć i / lub obliczyć pierwiastek kwadratowy z liczby, wystarczy wpisać 2 w polu indeksu i liczbę, z której chcesz wyciągnąć pierwiastek kwadratowy w polu radicand. Pamiętaj jednak, że możesz obliczyć i uprościć rodniki dowolnego indeksu i dowolnej liczby, pierwiastków 3 stopnia (Pierwiastek sześcienny), pierwiastków 4 stopni, itd.
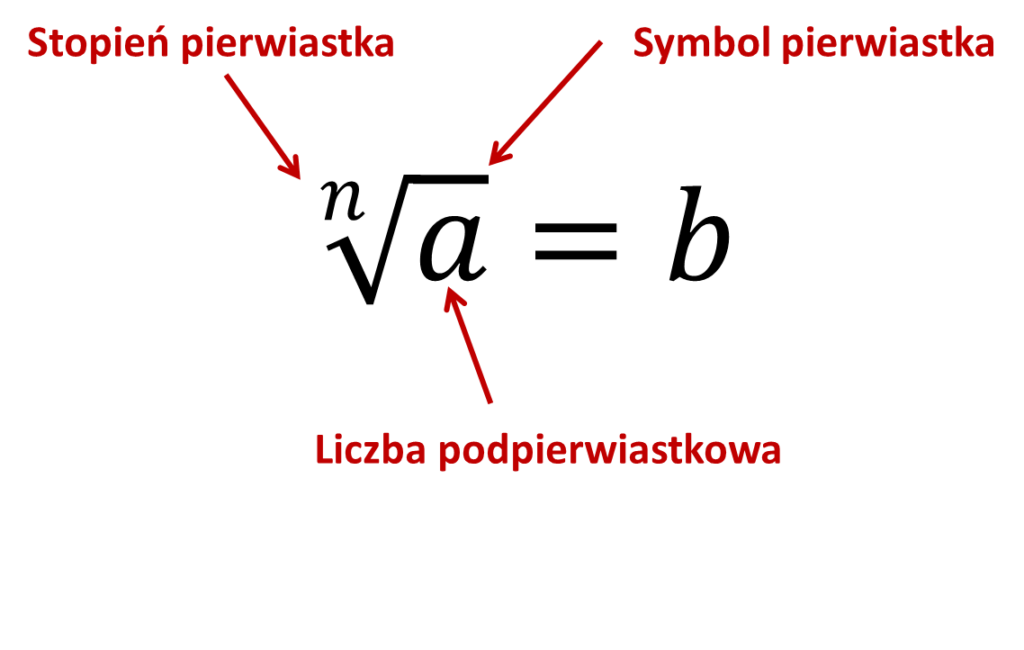
Potęgowanie i pierwiastkowanie
Rodnik lub pierwiastek jest matematycznym przeciwieństwem wykładnika, w tym samym sensie, w jakim dodawanie jest przeciwieństwem odejmowania. Potęgowanie można zdefiniować jako operację matematyczną, która reprezentuje mnożenie równych czynników. Oznacza to, że używamy potęgowania, gdy liczba jest mnożona przez siebie kilka razy.
Termin radykalny w świecie matematyki odnosi się do procesu matematycznego, który pozwala znaleźć pierwiastek liczby. A z kolei pierwiastek liczby x (radicand) to kolejna liczba, która pomnożona przez siebie określoną liczbę razy (według indeksu) jest równa x. Na przykład drugi pierwiastek 9 to 3, ponieważ 3 × 3 = 9.
Najmniejszy pierwiastek to pierwiastek kwadratowy, reprezentowany przez symbol √ który zwyczajowo pomija się jego stopień. Kolejny pierwiastek to pierwiastek sześcienny, reprezentowany przez symbol ³√. Mała liczba przed radykałem to Twój numer indeksu. Numer indeksu może być dowolną liczbą całkowitą i reprezentuje również wykładnik, którego można użyć do anulowania tego pierwiastka. Na przykład podniesienie do potęgi 3 anuluje pierwiastek sześcienny.
Ogólne zasady Pierwiastkowania | kalkulator pierwiastków
1. Wynik radykalnej operacji jest dodatni, jeśli liczba pod rodnikiem jest dodatnia.
2. Wynik jest ujemny, jeśli liczba pod rodnikiem jest ujemna, a liczba indeksu jest nieparzysta.
3. Liczba ujemna pod rodnikiem o parzystej liczbie indeksowej daje liczbę niewymierną.
4. Pamiętaj, że chociaż tego nie pokazano, indeks pierwiastka kwadratowego to 2.
.
Uproszczenie pierwiastków kwadratowych i innych rodników
Aby rozwiązać radykalne, konieczne jest poznanie pewnych zasad, które ułatwią radykalne uproszczenie. Tak jest w przypadku produktu i zasad ilorazu w pierwiastkowanie.
Pierwiastek iloczynu
Aby pomnożyć lub podzielić dwa rodniki, rodniki muszą mieć ten sam numer indeksu. Zasada iloczynu mówi, że mnożenie dwóch rodników po prostu mnoży wartości i umieszcza odpowiedź w obrębie tego samego typu rodnika, upraszczając, jeśli to możliwe. Na przykład,
³√4 x ³√2 =³√8, co można uprościć do 2, ponieważ 2 podniesione do 3 równa się 8. Ta zasada może również działać odwrotnie, dzieląc większy rodnik na dwie wielokrotności mniejszych rodników.
Pierwiastek ilorazu
Reguła ilorazu mówi, że podział jednego pierwiastka przez drugiego jest tym samym, co dzielenie liczb i umieszczanie ich pod tym samym symbolem rodnika. Na przykład,
√2/√4 =√2/4, Podobnie jak w przypadku reguły iloczynu, można również odwrócić regułę ilorazu, aby podzielić ułamek rodnika na dwa osobne rodniki.
Jak uprościć rodników
Niektóre pierwiastki można łatwo rozwiązać, ponieważ liczba wewnętrzna rozkłada się na liczbę całkowitą, na przykład √9 = 3. Ale większość nie uprości się tak wyraźnie. Reguła iloczynu może być użyta w odwrotnej kolejności, aby uprościć bardziej skomplikowane rodniki. Na przykład √27 jest również równe √9 × √3, ponieważ 27 to to samo, co powiedzenie 9×3, a ponieważ √9 = 3, ten problem można uprościć do 3√3. Można to zrobić nawet wtedy, gdy zmienna jest poniżej radykalnej, chociaż zmienna musi pozostać poniżej radykalnej.
Oto kroki, które musisz podjąć, aby uprościć radykały:
1. Musisz zainicjować liczbę wewnątrz rodnika. Zacznij od podzielenia liczby przez pierwszą liczbę pierwszą 2 i kontynuuj dzielenie przez 2, aż uzyskasz ułamek dziesiętny lub resztę, a następnie podziel przez 3, 5, 7 itd., aż jedyne liczby, które pozostaną, będą liczbami pierwszymi. Jeśli oryginalna liczba jest liczbą pierwszą, radykał nie może być uproszczony. Uwzględnij również dowolną zmienną w radykalnej.
2. Określ indeks rodnika. Indeks mówi, pod którym wykładnikiem należy pogrupować liczby pierwsze, aby otrzymać je jako współczynniki poza pierwiastkiem. Na przykład, jeśli indeks wynosi 2 (pierwiastek kwadratowy), to musisz pogrupować liczby pierwsze w potęgach z wykładnikiem 2, do tego wymagane jest, aby istniały dwie liczby pierwsze o tej samej wartości. Jeśli indeks wynosi 3 (do pierwiastka sześciennego), to potrzebujesz trójki, aby odsunąć liczbę pierwszą od pierwiastka.
3. Wyjmij jako współczynniki wszystkie liczby, które zgrupowałeś jako potęgi z wykładnikiem równym indeksowi pierwiastka.
4. Uprość wyrażenia, zarówno wewnątrz, jak i na zewnątrz radykału, mnożąc terminy. Pomnóż wszystkie liczby i zmienne w radykalnej razem. Pomnóż wszystkie liczby i zmienne poza radykałem.
Zrobione z ❤